Rumus Keliling dan Luas Segitiga Siku Siku

Daftar Isi

smarteduka.com – Halo sabahat smarteduka.com Pada postingan sebelumnya di laman smarteduka.com mimin sudah pernah memposting Rumus Luas dan Keliling Lingkaran serta contoh soal lingkaran dan pembahasannya. kali ini mimin smarteduka.com bakal ngebahas pengertian segitiga siku siku, sifat dan ciri ciri segitiga siku siku, rumus segitiga siku-siku, keliling segitiga siku siku, luas segitiga siku siku disertai contoh penyelesaian soal segitiga siku siku. untuk melihat tulisan lengkapnya bisa anda simak dibawah ini.

Pengertian Segitiga Siku-Siku

Segitiga siku-siku adalah segitiga yang satu sudutnya sebesar 90° (tegak lurus / siku-siku). Di dalam bahasa Inggris disebut dengan right triangle atau or right-angled triangle, dan dahulu disebut rectangled triangle. untuk lebih jelasnya berikut ini admin smarteduka.com menyajikan gambar seigitiga siku siku.

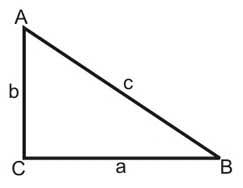
Sifat dan Ciri-Ciri Segitiga Siku-Siku

sifat dan ciri-ciri segitiga siku di kelompokkan dalam 3 hal yang umum yaitu :

Mempunyai 2 sisi yang saling tegak lurus
Memiliki satu sisi miring dan salah satu sudutnya yaitu sudut siku siku
Mempunyai simetri lipat dan simetri putar

Rumus Luas Segitiga Siku

L = ½ x alas . tinggi

dari gambar diatas yang merupakan bagian alas adalah sisi a atau panjang sisi CB, sedangkan yang merupakan tinggi adalah sisi b atau panjang sisi AC dan sisi miring adalah c atau panjang sisi AB.

Rumus Keliling Segitiga Siku

Keliling = sisi1 + sisi2 + sisi3

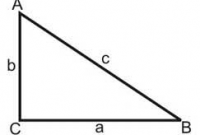
yang merupakan sisi1 adalah panjang sisi b, sedangkaan sisi2 adalah panjang sisi a dan sisi3 adalah panjang sisi c. jadi kesimpulannya bisa juga rumus keliling kita tuliskan dengan

Keliling = sisi a + sisi b + sisi c

tentunya untuk menghitung keliling kita harus tahu bagaimana cara mencari panjang sisi miringnya (sisi c). untuk mengetahui panjang dari sisi c maka kita harus mengetahui tentang rumus pythagoras. adapun pembahasan tentang rumus pythagoras bisa sahabat smarteduka.com baca dibawah ini.

Rumus Pythagoras

Rumus pythagoras atau lebih dikenal lagi dengan nama teorema pythagoras ataupun dalil pythagoras.

“Di dalam segitiga siku siku, ukuran sisi terpanjang atau sisi miring sama dengan kuadrat dari sisi lainnya.”

atau kalau kita gambarkan kedalam sebuah Berikut adalah rumusnya:

a² + b² = c²

Umumnya rumus pythagoras berguna untuk menghitung hal yang bersifat geometri. Misalnya dipakai untuk mencari keliling segitiga siku siku yang panjang sisi miringnya belum diketahui. Untuk lebih memahami rumus pythagoras, Simak melalui gambar segitiga di bawah ini.

Berdasarkan gambar diatas bsa didapat rumus pythagoras seperti di bawah ini :

BC² = AC² + AB²

Ada juga rumus pythagoras yang berfungsi untuk mencari sisi alas atau sisi samping tinggi atau sisi miring.

Mencari sisi alas
b² = c² – a²

Mencari sisi samping tinggi
a² = c² – a²

Contoh Soal

Contoh Soal 1: Mencari Panjang Sisi Miring Segitiga Siku-Siku Diketahui sebuah segitiga siku-siku memiliki panjang sisi sejajar dengan alas sebesar 5 cm dan panjang sisi tegak sebesar 12 cm. Tentukan panjang sisi miring segitiga tersebut!

Penyelesaian: Diberikan:

Panjang sisi sejajar dengan alas (a) = 5 cm
Panjang sisi tegak (b) = 12 cm

Rumus Pythagoras: c² Substitusi nilai yang diberikan:

c² = 5² + 12²; c² = 25 + 144; c² = 169; c = √169; c = 13

Jadi, panjang sisi miring segitiga siku-siku tersebut adalah 13 cm.

Contoh Soal 2: Mencari Panjang Sisi Sejajar dengan Alas Diketahui sebuah segitiga siku-siku memiliki panjang sisi miring sebesar 10 cm dan panjang sisi tegak sebesar 8 cm. Tentukan panjang sisi sejajar dengan alas segitiga tersebut!